(ENEM PPL - 2019)No trapzio issceles mostrado na f
(ENEM PPL - 2019)
No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.
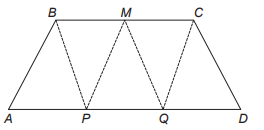
Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura. A razão entre \(\overline{BC}\) e \(\overline{AD}\)que determina áreas iguais para os cinco triângulos mostrados na figura é
A
\(\frac{1}{3}\)
B
\(\frac{2}{3}\)
C
\(\frac{2}{5}\)
D
\(\frac{3}{5}\)
E


